N(B) = anan-1...a1a0
représente en fait le nombre décimal :
N = an × Bn + an-1 × Bn-1 + ... + a1 × B1 + a0 × B0
ou
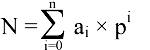
Tous les composants des ordinateurs et autres calculateurs utilisent seulement deux états : absence ou passage d'un courant, condensateur chargé ou déchargé, etc. Ce sont des phénomènes binaires. Le traitement d'informations par un ordinateur demande le codage des informations sous la forme de phénomènes physiques à deux états. Les travaux du mathématicien allemand Gottfried Wilheim Leibniz (1646 -1716), un des premiers spécialistes de la numération et de l'arithmétique binaire, et du mathématicien britannique George Boole (1815 -1864) sont à la base du traitement des nombres sous forme binaire. Ce système de numération n'utilise que deux symboles : 0 et 1 en raison des deux états physiques.
Nous utilisons généralement le système décimal ou système à base 10. Son alphabet est constitué de dix chiffres : 0; 1; 2; 3; 4; 5; 6; 7; 8 et 9. On peut écrire tous les nombres en attribuant à chaque unité de rang la valeur de dix unités du rang immédiatement inférieur.
| Exemple: | ||||
| 1984 | = 1000 | + 900 | + 80 | + 4 |
| = 1 × 1000 | + 9 × 100 | + 8 × 10 | + 4 × 1 | |
| = 1 × 103 | + 9 × 102 | + 8 × 101 | + 4 × 100 | |
Le système décimal associe donc à chaque rang un poids fixe (100 pour le rang 0, 101 pour le rang 1, ..., 10n pour le rang n). On dit que ce code est pondéré. Il existe des codes non-pondérés, par exemple, le code utilisé par les chiffres romains.
En généralisant, on observe, pour tout système
de numération pondéré à base B, qu'il existe un
alphabet composé de B chiffres différents, et que le poids attribué
à un rang est de B élevé à la puissance du numéro
de rang. Donc un nombre exprimé en base B sous la forme d'une suite de
n+1 chiffres :
N(B) = anan-1...a1a0
représente en fait le nombre décimal :
N = an × Bn + an-1 × Bn-1
+ ... + a1 × B1 + a0 × B0
ou
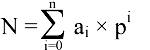
Le nombre dans une base particulière est noté différemment : soit on le fait suivre du numéro de base ou de la première lettre du nom du système de numération (O pour octale, B pour binaire, H pour hexadécimal,...) entre parenthèse et en indice, par exemple, 25(8), ou 11101(B), soit on le précède de la lettre symbolisant la base et d'un apostrophe, par exemple H' FF ou B' 1001.
Le système binaire, ou système à base 2, respecte totalement cette numération. Les chiffres binaires sont appelés généralement bits (binary digit).
Exemple :
10111(2) = 1 × 24 + 0 × 23 + 1
× 22 + 1 × 21 + 1 × 20
10111(2) = 16 + 0 + 4 +2 +1
10111(2) = 23
Il existe d'autres systèmes couramment utilisés en informatique le système octal (B=8) et le système hexadécimal (B=16, l'alphabet est composé de 16 "chiffres" 0, 1, 2, 3, 4, 5, 7, 8, 9, A, B, C, D, E, F).
| Système décimal | Système binaire | Système octal | Système hexadécimal |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Exemple de conversion : 17
|
Rang
|
||||||
|
17
|
: 2 = | 8 | reste | 1 |
|
0
|
|
8
|
: 2 = | 4 | reste | 0 |
1
|
|
|
4
|
: 2 = | 2 | reste | 0 |
2
|
|
|
2
|
: 2 = | 1 | reste | 0 |
3
|
|
|
1
|
: 2 = | 0 | reste | 1 |
4
|
|
Donc 17(10) = 10001(2).
Vu la quantité importante d'information que les ordinateurs doivent traiter, il a fallu grouper les bits par 8, en octet (symbole o). Des multiples ont été crées rapidement mais en commettant une erreur :
| Ab. | Nom | Valeur | ||
|---|---|---|---|---|
| o | octet | 8 bits | ||
| Ko | kilo-octet | 210 o | au lieu de | 103 |
| Mo | méga-octet | (210)2 o | 106 | |
| Go | giga-octet | (210)3 o | 109 | |
| To | téra-octet | (210)4 o | 1012 | |
| Po | péta-octet | (210)5 o | 1015 | |
| Eo | exa-octet | (210)6 o | 1018 | |
| Zo | zetta-octet | (210)7 o | 1021 | |
| Yo | yotta-octet | (210)8 o | 1024 |
Un octet permet de stocker 8 bits ou 4 chiffres octales ou 2 chiffres hexadécimaux.
Cette erreur, qui parait peut importante au niveau du kilo-octet, devient rapidement conséquente. C'est pour quoi les comités scientifiques de divers pays, on eu l'idée de créer un système de préfixe spéciale en utilisant les deux premières lettres du préfixe standard et en y ajoutant "bi" : un kibi-octet (Kio) = 1024 octets, un mébi-octet (Mio) = (210)2,... Mais, au jour d'aujourd'hui, ces recommandations ne sont respectées ni par les particuliers ni par les entreprises.
Une couleur est codée de différente manière en fonction du matériel cible (moniteur, imprimante, etc.).
 Le
RGB utilise les trois couleurs des photophores, les petites pastilles qui deviennent
luminescente sous l'effet des électrons, de l'écran de l'ordinateur
ou de la télévision : le rouge (Red), le vert (Green) et le bleu
(Blue). C'est pourquoi ce système est parfois traduit par RGB. L'œil
à une distance normale ne peut différencier ces points et mélange
ces trois couleurs pour en donner une seule. Les couleurs de la lumière
sont additives, c'est-à-dire que l'on part du noir pour arriver à
une couleur toujours plus claire.
Le
RGB utilise les trois couleurs des photophores, les petites pastilles qui deviennent
luminescente sous l'effet des électrons, de l'écran de l'ordinateur
ou de la télévision : le rouge (Red), le vert (Green) et le bleu
(Blue). C'est pourquoi ce système est parfois traduit par RGB. L'œil
à une distance normale ne peut différencier ces points et mélange
ces trois couleurs pour en donner une seule. Les couleurs de la lumière
sont additives, c'est-à-dire que l'on part du noir pour arriver à
une couleur toujours plus claire.
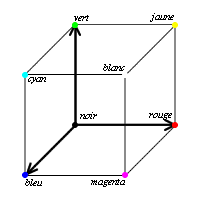 On
peut imaginer un cube contenant tout les couleurs. Le système RGB est
un système de forme cubique.
On
peut imaginer un cube contenant tout les couleurs. Le système RGB est
un système de forme cubique.
Généralement chaque composante est codée sur trois octets. On attribut par conséquent à chaque couleur un nombre entre 0 et 255 (FF en hexadécimal).
Quelques exemples de couleurs :
Blanc : R=255; G=255; B=255
Jaune : R=255; G=255; B=0
Les imprimantes à jet d'encre utilisent 4 encres différentes, les trois couleurs primaires (Cyan, Magenta, Jaune) et le noir. Au contraire de la lumière, les couleurs de la matière sont soustractive, c'est-à-dire que l'on part du blanc pour arriver au noir.
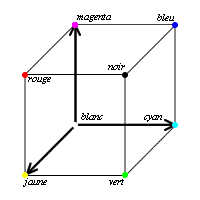

Pour noter les couleurs, suivant les logiciels, on note chaque terme en pourcentage ou sur l'intervalle [0;255] comme pour le RVB.
On note une couleur soit par les valeur de C, M et Y :
C 1 M 1 Y 0 = Bleu
C 0,5 M 1 Y 1 = Rouge foncé
soit par les valeurs C, M, Y, K (pour blacK, noir) :
C' 1 M' 1 Y' 0 K 0 = Bleu
C' 0 M' 0,5 Y' 0,5 K 0,5 = Rouge foncé
Donc K = min (C, M, Y) et ![]() .
.
Théoriquement pour convertir une couleur RGB
en CMY, il suffit d'appliquer cette formule :![]() .
.
Mais à cause des problèmes de rendus papier les logiciels de graphisme préfèrent utiliser des formules plus complexes pour réduire l'écart Écran/Imprimante. Ces logiciels veulent être WYSIWIG.
Le HSL (Hue, Saturation, Luminance) : 2 concepts selon les logiciels, donc 2 formes.

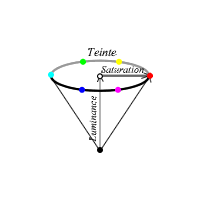
On range les couleurs de la manière suivante: sur la périphérie, on place les couleurs d'un spectre légèrement différent du spectre de la lumière visible.
![]()
La teinte passe ainsi successivement par les couleurs du spectre: rouge, orange, jaune, vert, cyan, bleu, indigo, violet, magenta... On repère la couleur par un angle, variant de 0° à 360°: le rouge est à 0°, le jaune à 60°, le vert 120°, le cyan 180°, le bleu 240° et le magenta 300°.
Pour le double cône, arrêtons-nous à l'angle 0° au rouge. Toutes les couleurs du triangle présentent la même teinte, mais varient en saturation et en luminosité. Plus on s'approche de l'axe central de la toupie, plus les rouges sont fades: ils sont peu saturés. Plus on s'en éloigne, plus les rouges sont vifs: ils sont saturés. En se promenant de bas en haut, on observe que les couleurs du bas sont sombres (peu lumineuses) et celles du haut, claires (lumineuses). Il en va ainsi pour toutes les tranches de la toupie, c'est-à-dire pour chacune des teintes.
Pour le simple cône, le principe est peu différent. Le blanc est considéré comme une couleur normale, c'est-à dire qu'il n'est pas plus lumineux qu'un rouge. La saturation 0 transforme un rouge lumineux en blanc.
L'intérêt d'un tel classement, c'est qu'il offre une approche "humaine" à la recherche d'une couleur. Lorsqu'on essaye de décrire une couleur, on donne naturellement (et sans s'en rendre compte) sa teinte, sa saturation et sa luminosité. Ainsi, on décrit le brun comme étant un "orange foncé et légèrement pâle": teinte (orange), luminosité (foncé), et saturation (légèrement pâle).
Les palettes sont des listes de couleurs particulières. Par exemple, si on utilise quatre couleurs seulement, au lieu de nommer à chaque fois la couleur en RGB, on met nos quatre couleurs dans une palette à laquelle, on fait référence à une couleur par son emplacement dans la liste, son index. L'indexation des couleurs permet de réduire la taille des images.
Les palettes courantes sont la palette de Windows, celle de MacOS et la palette dîtes Web. La palette Windows (256 couleurs), et la palette MacOS (256) résultent des longues évolutions des systèmes d'exploitation et ne sont pas vraiment très utiles pour des images modernes. Par contre la palette "Web" sécurisée est au contraire très logique. Pour simplifier, elle a été créée avec 216 couleurs seulement pour libérer, pour les autres applications du système, de l'espace dans la mémoire des cartes graphiques d'ancienne génération qui n'accepte que des index de couleurs sur 8 bits soit 256 index (28) de couleurs possibles. Ces couleurs ont été choisies parce que chaque valeur RVB est multiple de 51 ou 33(16).
La palette sécurisée en hexadécimal (RRVVBB):
| FF0000 | FF0033 | FF0066 | FF0099 | FF00CC | FF00FF |
| FF3300 | FF3333 | FF3366 | FF3399 | FF33CC | FF33FF |
| FF6600 | FF6633 | FF6666 | FF6699 | FF66CC | FF66FF |
| FF9900 | FF9933 | FF9966 | FF9999 | FF99CC | FF99FF |
| FFCC00 | FFCC33 | FFCC66 | FFCC99 | FFCCCC | FFCCFF |
| FFFF00 | FFFF33 | FFFF66 | FFFF99 | FFFFCC | FFFFFF |
| CC0000 | CC0033 | CC0066 | CC0099 | CC00CC | CC00FF |
| CC3300 | CC3333 | CC3366 | CC3399 | CC33CC | CC33FF |
| CC6600 | CC6633 | CC6666 | CC6699 | CC66CC | CC66FF |
| CC9900 | CC9933 | CC9966 | CC9999 | CC99CC | CC99FF |
| CCCC00 | CCCC33 | CCCC66 | CCCC99 | CCCCCC | CCCCFF |
| CCFF00 | CCFF33 | CCFF66 | CCFF99 | CCFFCC | CCFFFF |
| 990000 | 990033 | 990066 | 990099 | 9900CC | 9900FF |
| 993300 | 993333 | 993366 | 993399 | 9933CC | 9933FF |
| 996600 | 996633 | 996666 | 996699 | 9966CC | 9966FF |
| 999900 | 999933 | 999966 | 999999 | 9999CC | 9999FF |
| 99CC00 | 99CC33 | 99CC66 | 99CC99 | 99CCCC | 99CCFF |
| 99FF00 | 99FF33 | 99FF66 | 99FF99 | 99FFCC | 99FFFF |
| 660000 | 660033 | 660066 | 660099 | 6600CC | 6600FF |
| 663300 | 663333 | 663366 | 663399 | 6633CC | 6633FF |
| 666600 | 666633 | 666666 | 666699 | 6666CC | 6666FF |
| 669900 | 669933 | 669966 | 669999 | 6699CC | 6699FF |
| 66CC00 | 66CC33 | 66CC66 | 66CC99 | 66CCCC | 66CCFF |
| 66FF00 | 66FF33 | 66FF66 | 66FF99 | 66FFCC | 66FFFF |
| 330000 | 330033 | 330066 | 330099 | 3300CC | 3300FF |
| 333300 | 333333 | 333366 | 333399 | 3333CC | 3333FF |
| 336600 | 336633 | 336666 | 336699 | 3366CC | 3366FF |
| 339900 | 339933 | 339966 | 339999 | 3399CC | 3399FF |
| 33CC00 | 33CC33 | 33CC66 | 33CC99 | 33CCCC | 33CCFF |
| 33FF00 | 33FF33 | 33FF66 | 33FF99 | 33FFCC | 33FFFF |
| 000000 | 000033 | 000066 | 000099 | 0000CC | 0000FF |
| 003300 | 003333 | 003366 | 003399 | 0033CC | 0033FF |
| 006600 | 006633 | 006666 | 006699 | 0066CC | 0066FF |
| 009900 | 009933 | 009966 | 009999 | 0099CC | 0099FF |
| 00CC00 | 00CC33 | 00CC66 | 00CC99 | 00CCCC | 00CCFF |
| 00FF00 | 00FF33 | 00FF66 | 00FF99 | 00FFCC | 00FFFF |