Animation Flash
(animation vectorielle spécialisée
pour le Web)
Une image vectorielle est un ensemble de formes, dont toutes les caractéristique sont fixés : type (polygone, ovale, courbe, ...), la position des points qui le composent, sa couleur, son motif, etc. . Par opposition aux images bitmap, un cercle n'est pas défini par des pixels mais par ses caractéristiques. La position des points est donné en fonction d'un repère du plan où l'axe des ordonnées (yy') est inversé par rapport à l'habitude des mathématiciens.
Par exemple, une image (comme un cercle par exemple) de petite taille que l'on grossit dix fois, le cercle est agrandit mais il n'est pas déformé car la précision de l'image ne dépend pas du facteur d'agrandissement (contrairement au bitmap).
|
Animation Flash |
Ils existent différent formats utilisant ce système :
Les formes sont donc les possibilités offertes aux graphiste
pour créer leur image. On trouve toutes les formes traditionnelles :
segments, cercles, polygones en tous genres.
Mais on trouve des formes beaucoup moins traditionnels mais plus "naturelles".
Par exemple, les ellipses remplacent avantageusement un cercle, et une courbe
de Bezier permet de reproduire des courbes rapidement.
L'équation paramétrique d'un cercle de centre O et de rayon R est x = xO + R cos t et y = yO + R sin t, ce qui se déduit du cercle trigonométrique. Mais une ellipse a deux "rayons" : le demi-grand axe pour les abscisses, le demi-petit axe pour les ordonnées. Donc l'équation paramétrique de l'ellipse de centre O et de demi-grand axe a et de demi-petit axe b est { x = a cos t ; y = b sin t } où la variable t varie entre 0 et 2 π.
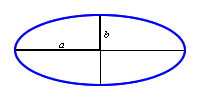
Les ellipses sont caractérisées dans les logiciels de dessin vectoriel par un rectangle. L'ellipse est inscrite dans ce rectangle.
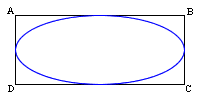
Donc l'équation paramétrique est x = xA + (xB - xA) / 2 cos t et y = yA + (yD - yA) / 2 sin t
Pierre
Bezier (1910-1999), ingénieur des Arts et Métiers, travaillait
à la régie Renault, quand il "inventa" en 1970 des courbes
particulières qui porte maintenant son nom. Ce fut le début de
CAO, DAO.
Au départ, il devait trouver un moyen simple pour reproduire sur ordinateur des courbes tracé à main-levée par des dessinateurs. Il retravailla certaines études de Paul Faget de Casteljau, ingénieur travaillant chez Citroën, c'est pourquoi on utilise "l'algorithme de Casteljau" pour les tracer. Aujourd'hui ses courbes sont utilisées dans le monde entier sans vraiment savoir d'où vient cet appellation.
Ces courbes se singularisent par des points de contrôle. Deux points définissent les limites de la courbes et un ou deux points la forme de la courbes.
L'algorithme de Casteljau consiste à une succession de barycentre pour obtenir un point qui appartiendra à la courbe pour t compris [0;1].
On construit une courbe de Bezier de degré n à partir d'un polygone appelépolygone descripteur à n+1 sommets { P0, ... , Pn} appelés points de contrôle.
Pour une courbe de Bezier de degré 3, on construit les barycentres suivants le schéma ci-dessous :
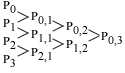Soit
P0,1 le barycentre de (P0, 1-t) et (P1, t)
Soit P1,1 le barycentre de (P1, 1-t) et (P2, t)
Soit P2,3 le barycentre de (P2, 1-t) et (P3, t)
Soit P0,2 le barycentre de (P0,1, 1-t) et (P1,1, t)
soit P1,2 le barycentre de (P1,1, 1-t) et (P2,1, t)
soit P0,3 le barycentre de (P0,2, 1-t) et (P1,2, t)
Le dernier point décrit donc la courbe de Bezier, quand t vari de 0 à 1.
On peut généraliser en parlant d'interpolation linéaire
à la place des barycentres. Chaque point intermédiaire Pi,j
est construit itérativement par une interpolation linéaire entre
les points Pi, (j-1) et P(i+1), (j-1)
:
Pi, j(t) = (1-t) Pi,
(j-1)(t) + t P(i+1), (j-1)
Le dernier point interpolé P0,n est donc le résultat de la combinaison
de 
interpolations linéaires et décrit une courbe de Bezier de degré
n : bn(t).